Symmetry

Ringing Homepage      Email me

	The different symmetries possible in change-ringing methods
	I became interested in method-symmetries when looking at cyclic methods, which cannot have conventional symmetry. Martin Bright has written the definitive article on method-symmetry, which can be found on his homepage. As Martin's article explains, a method with an even length can have one of eleven possible symmetry types; however, only nine are possible for valid, true methods. The following is a list of the nine, with details and an example grid for each type.
	Name: Conventional symmetry (vertical symmetry about a change / palindromic symmetry) This is by far the most common type of symmetry in methods. Example given: Single Oxford Bob Major Notation: -14-16-18-18-18-16-14-12 The notation is palindromic (reads the same forwards or backwards) about the mid-point (the half-lead), with the exception of the leadhead change. Other Examples: Plain Bob, Cambridge Surprise
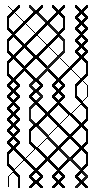
	Name: Glide symmetry (skew symmetry) First used in 1752, it has become popular recently due to its use in cyclic methods. Methods with this symmetry have no distinct reverse. Example given: Double Cambridge Cyclic Bob Notation: -16-16-18-78-38-38-18-12 After the half-lead, the notation from the first half is used from the beginning in the same order, but reversed. Other Examples: Double Eastern Bob, Olympus Surprise
	Name: Rotational symmetry This has also been used recently in cyclic methods. The grid is the same when rotated through 180 degrees. Example given: Anglia Cyclic Bob Notation: -18-123678-18-78-58-36-14-12 Moving out both ways from either quarter-lead (here the 123678 and the 36), the notations are the reverses of each other. Other Examples: Brave New World Cyclic Bob, Nimrod Surprise.
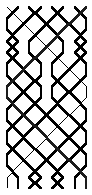
	Name: Horizontal symmetry A method with only this type of symmetry has never been rung. Methods must be twin-hunt with this symmetry. Example given: Unnamed Bob Major Notation: -18-36-1458-1458-18-18-18-1278 Only horizontally symmetric notations are allowed. On eight bells, this means only x,18,1278,1458,123678 & 36 are allowed. Other Examples: -18-36-18-18-18-18-18-1278
	Name: Mirror symmetry This is horizontal symmetry, with conventional (palindromic) symmetry as well. Again. methods must be twin-hunt with this symmetry. Example given: Bucknell Bob Major Notation: -18-36-18.36.18.36.18-36-18-1278 Again, only horizontally symmetric notations are allowed. Other Examples: Mirror Bob
	Name: Double symmetry This is conventional (palindromic) symmetry as well, with rotational symmetry about each quarter-lead. Example given: Double Oxford Bob Major Notation: -14-36-58-78-58-36-14-12 The notation can be thought of as conventional symmetry with quarter-lead rotations. Other Examples: Bristol Surprise, Double Bob
	Name: Vertical (about a row) This is only one valid method possible with this symmetry. Example given: Cross Differential Notation: - The method is symmetrically very pure. Other Examples: n/a
	Name: Asymmetric There is no symmetry present in these methods. Example given: Eastern Bob Notation: -14-38-18-18-18-18-18-12 Other Examples: Selenium Surprise, Quasar